3. The framework architecture¶
3.1. Overview¶
In this chapter we outline some of the main features of the Gaudi architecture. A (more) complete view of the architecture, along with a discussion of the main design choices and the reasons for these choices may be found in references [LHCB-98-064] and [Barrand:467678].
3.2. Why architecture?¶
The basic “requirement” of the physicists is a set of programs for doing event simulation, reconstruction, visualisation, etc. and a set of tools which facilitate the writing of analysis programs. Additionally a physicist wants something that is easy to use and (though he or she may claim otherwise) is extremely flexible. The purpose of the Gaudi application framework is to provide software which fulfils these requirements, but which additionally addresses a larger set of requirements, including the use of some of the software online.
If the software is to be easy to use it must require a limited amount of learning on the part of the user. In particular, once learned there should be no need to re-learn just because technology has moved on (you do not need to re-take your licence every time you buy a new car). Thus one of the principal design goals was to insulate users (physicist developers and physicist analysists) from irrelevant details such as what software libraries we use for data I/O, or for graphics. We have done this by developing an architecture. An architecture consists of the specification of a number of components and their interactions with each other. A component is a “block” of software which has a well specified interface and functionality. An interface is a collection of methods along with a statement of what each method actually does, i.e. its functionality.
The main components of the Gaudi software architecture can be seen in the object diagram shown in Fig. 3.1. Object diagrams are very illustrative for explaining how a system is decomposed. They represent a hypothetical snapshot of the state of the system, showing the objects (in our case component instances) and their relationships in terms of ownership and usage. They do not illustrate the structure, i.e. class hierarchy, of the software.
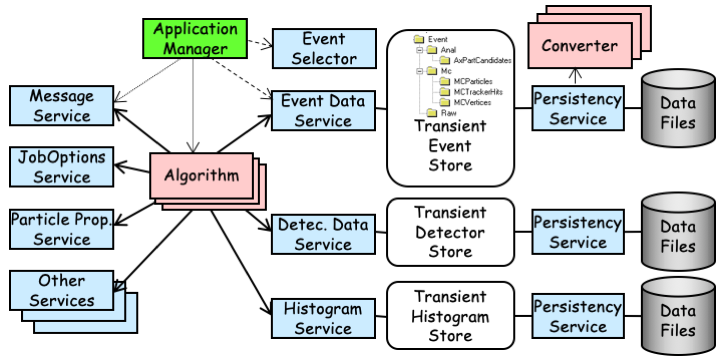
Fig. 3.1 Gaudi Architecture Object Diagram¶
It is intended that almost all software written by physicists, whether for event generation, reconstruction or analysis, will be in the form of specialisations of a few specific components. Here, specialisation means taking a standard component and adding to its functionality while keeping the interface the same. Within the application framework this is done by deriving new classes from one of the base classes:
· DataObject· Algorithm· ConverterIn this chapter we will briefly consider the first two of these components and in particular the subject of the “separation” of data and algorithms. They will be covered in more depth in chapters Section 6 and Section 7. The third base class, Converter, exists more for technical necessity than anything else and will be discussed in Section 14. Following this we give a brief outline of the main components that a physicist developer will come into contact with.
3.3. Data versus code¶
Broadly speaking, tasks such as physics analysis and event reconstruction consist of the manipulation of mathematical or physical quantities: points, vectors, matrices, hits, momenta, etc., by algorithms which are generally specified in terms of equations and natural language. The mapping of this type of task into a programming language such as FORTRAN is very natural, since there is a very clear distinction between “data” and “code”. Data consists of variables such as:
integer n real p(3)and code which may consist of a simple statement or a set of statements collected together into a function or procedure:
real function innerProduct(p1, p2) real p1(3), p2(3) innerProduct = p1(1) * p2(1) + p1(2) * p2(2) + p1(3) * p2(3) endThus the physical and mathematical quantities map to data and the algorithms map to a collection of functions.
A priori, we see no reason why moving to a language which supports the idea of objects, such as C++, should change the way we think of doing physics analysis. Thus the idea of having essentially mathematical objects such as vectors, points etc. and these being distinct from the more complex beasts which manipulate them, e.g. fitting algorithms etc. is still valid. This is the reason why the Gaudi application framework makes a clear distinction between “data” objects and “algorithm” objects.
Anything which has as its origin a concept such as hit, point, vector, trajectory, i.e. a clear “quantity-like” entity should be implemented by deriving a class from the DataObject base class.
On the other hand anything which is essentially a “procedure”, i.e. a set of rules for performing transformations on more data-like objects, or for creating new data-like objects should be designed as a class derived from the Algorithm base class.
Further more you should not have objects derived from DataObject performing long complex algorithmic procedures. The intention is that these objects are “small”.
Tracks which fit themselves are of course possible: you could have a constructor which took a list of hits as a parameter; but they are silly. Every track object would now have to contain all of the parameters used to perform the track fit, making it far from a simple object. Track-fitting is an algorithmic procedure; a track is probably best represented by a point and a vector, or perhaps a set of points and vectors. They are different.
3.4. Main components¶
The principle functionality of an algorithm is to take input data, manipulate it and produce new output data. Fig. 3.2 shows how a concrete algorithm object interacts with the rest of the application framework to achieve this.
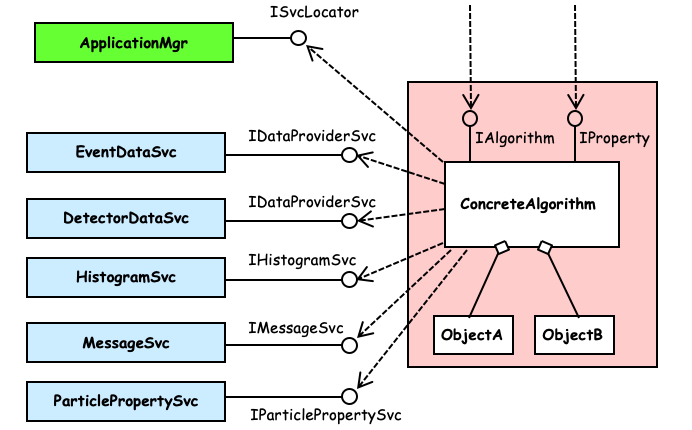
Fig. 3.2 The main components of the framework as seen by an algorithm object¶
The figure shows the four main services that algorithm objects use:
· The event data store· The detector data store· The histogram service· The message serviceThe particle property service is an example of additional services that are available to an algorithm. The job options service (see Section 12) is used by the Algorithm base class, but is not usually explicitly seen by a concrete algorithm.
Each of these services is provided by a component and the use of these components is via an interface. The interface used by algorithm objects is shown in the figure, e.g. for both the event data and detector data stores it is the IDataProviderSvc interface. In general a component implements more than one interface. For example the event data store implements another interface: IDataManagerSvc which is used by the application manager to clear the store before a new event is read in.
An algorithm’s access to data, whether the data is coming from or going to a persistent store or whether it is coming from or going to another algorithm is always via one of the data store components. The IDataProviderSvc interface allows algorithms to access data in the store and to add new data to the store. It is discussed further in Section 7 where we consider the data store components in more detail.
The histogram service is another type of data store intended for the storage of histograms and other “statistical” objects, i.e. data objects with a lifetime of longer than a single event. Access is via the IHistogramSvc which is an extension to the IDataProviderSvc interface, and is discussed in Section 10. The n-tuple service is similar, with access via the INtupleSvc extension to the IDataProviderSvc interface, as discussed in Section 11.
In general, an algorithm will be configurable: It will require certain parameters, such as cut-offs, upper limits on the number of iterations, convergence criteria, etc., to be initialised before the algorithm may be executed. These parameters may be specified at run time via the job options mechanism. This is done by the job options service. Though it is not explicitly shown in the figure this component makes use of the IProperty interface which is implemented by the Algorithm base class.
During its execution an algorithm may wish to make reports on its progress or on errors that occur. All communication with the outside world should go through the message service component via the IMessageSvc interface. Use of this interface is discussed in Section 12.
As mentioned above, by virtue of its derivation from the Algorithm base class, any concrete algorithm class implements the IAlgorithm and IProperty interfaces, except for the three methods initialize(), execute(), and finalize() which must be explicitly implemented by the concrete algorithm. IAlgorithm is used by the application manager to control top-level algorithms. IProperty is usually used only by the job options service.
The figure also shows that a concrete algorithm may make use of additional objects internally to aid it in its function. These private objects do not need to inherit from any particular base class so long as they are only used internally. These objects are under the complete control of the algorithm object itself and so care is required to avoid memory leaks etc.
We have used the terms “interface” and “implements” quite freely above. Let us be more explicit about what we mean. We use the term interface to describe a pure virtual C++ class, i.e. a class with no data members, and no implementation of the methods that it declares. For example:
class PureAbstractClass { virtual void method1() = 0; virtual void method2() = 0; };is a pure abstract class or interface. We say that a class implements such an interface if it is derived from it, for example:
class ConcreteComponent: public PureAbstractClass { void method1() {} void method2() {} };A component which implements more than one interface does so via multiple inheritance, however, since the interfaces are pure abstract classes the usual problems associated with multiple inheritance do not occur. These interfaces are identified by a unique number which is available via a global constant of the form: IID_InterfaceType, such as for example IID_IDataProviderSvc. Interface identifiers are discussed in detail in Section 17.
Within the framework every component, e.g. services and algorithms, has two qualities:
· A concrete component class, e.g. TrackFinderAlgorithm or MessageSvc.· Its name, e.g. “KalmanFitAlgorithm” or “MessageService”.
3.5. Controlling and Scheduling¶
3.5.1. Application Bootstrapping¶
The application is bootstrapped by creating an instance of the ApplicationMgr component. The ApplicationMgr is in charge of creating an initializing a minimal set of basic and essential services before control is given to specialized scheduling services. These services are shown in Fig. 3.3. The EventLoopMgr is in charge controlling the main physics event 1 loop and scheduling the top algorithms. There will be a number of more or less specialized implementations of EventLoopMgr which will perform the different actions depending on the running environment, and experiment specific policies (clearing stores, saving histograms, etc.). There exists the possibility to give the full control of the application to a component implementing the IRunable interface. This is needed for interactive applications such as event display, interactive analysis, etc. The Runable component can interact directly with the EventLoopMgr for triggering the processing of the next physics event.
The essential services that the ApplicationMgr need to instantiate and initialize are the MessageSvc and JobOptionsSvc.

Fig. 3.3 Control and Scheduling collaboration¶
3.5.2. Algorithm Scheduling¶
The Gaudi architecture foresees explicit invocation of algorithms by the framework or by other algorithms. This latter possibility allows for a hierarchical organization of algorithms, for example, a high level algorithm invoking a number of sub-algorithms.
The EventLoopMgr component is in charge of initializing, finalizing and executing the set of Algorithms that have been declared with the TopAlg property. These Algorithms are executed unconditionally in the order they have been declared. This vary basic scheduling is insufficient for many use cases (event filtering, conditional execution, etc.). Therefore, a number of Algorithms have been introduced that perform more sophisticated scheduling and can be configured by some properties. Examples are: Sequencers, Prescalers, etc. and the list can be easily extended. See Section 6.5 for more details on these generic high level Algorithms.
- 1
We state physics event to differentiate from what is called generally an event in computing.
